Blocos Dinâmicos de Primeira Ordem¶
Este caso exemplo ilustra o comportamento dinâmico dos blocos dinâmicos de primeira ordem mais utilizados no programa Anatem.
Dica
Entre os blocos de primeira ordem mais utilizados do Anatem, constam os blocos:
- PROINT
Bloco proporcional integral, cuja função de transferência é descrita por \(\frac{P_1+sP_2}{sP_3}\). Na definição deste bloco, os parâmetros \(P_1\) e \(P_3\) devem ser não nulos.
- WSHOUT
Bloco wash-out, cuja função de transferência é descrita por \(\frac{sP_1}{P_2+sP_3}\). Na definição deste bloco, os parâmetros \(P_1\), \(P_2\) e \(P_3\) devem ser não nulos.
- LEDLAG
Bloco avanço-atraso, cuja função de transferência é descrita por \(\frac{P_1+sP_2}{P_3+sP_4}\). Na definição deste bloco, os parâmetros \(P_1\), \(P_3\) e \(P_4\) devem ser não nulos.
Nota
De forma genérica, funções de transferência de primeira ordem podem ser modelados por meio do seguinte bloco:
O CDU ilustrado na Fig. 95 permite avaliar a resposta de blocos de primeira ordem ao degrau (representado pela função PULSO) com amplitude \(V\).
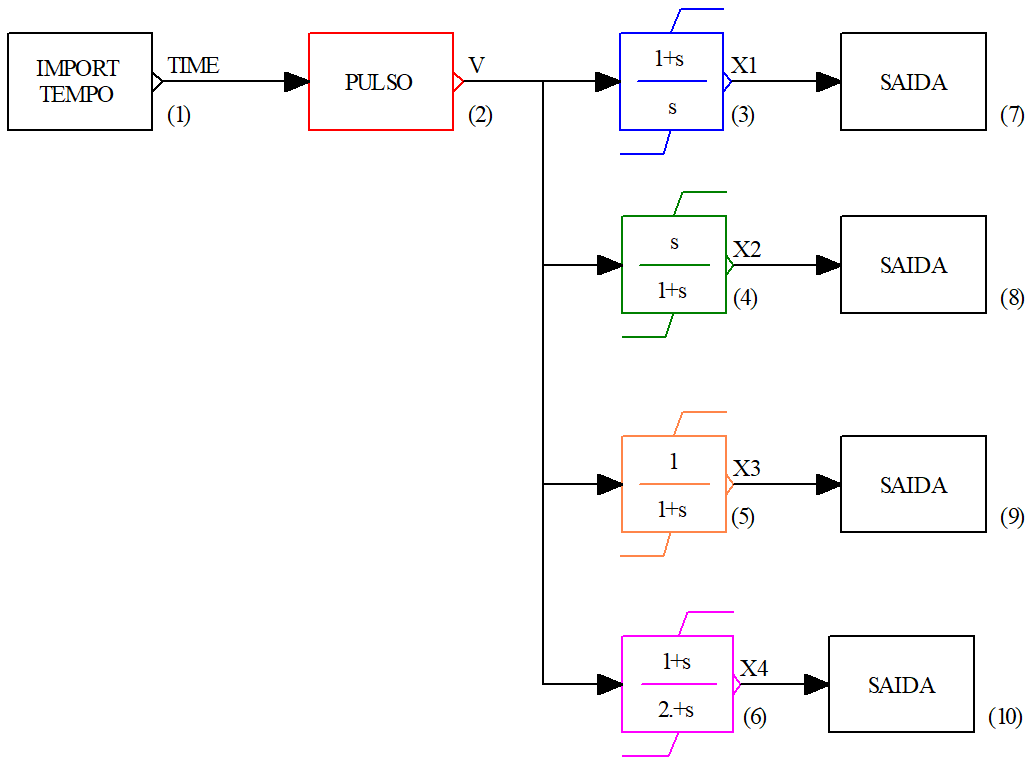
Fig. 95 Caso exemplo com blocos de primeira ordem¶
Os resultados desta simulação são apresentados na Fig. 96:
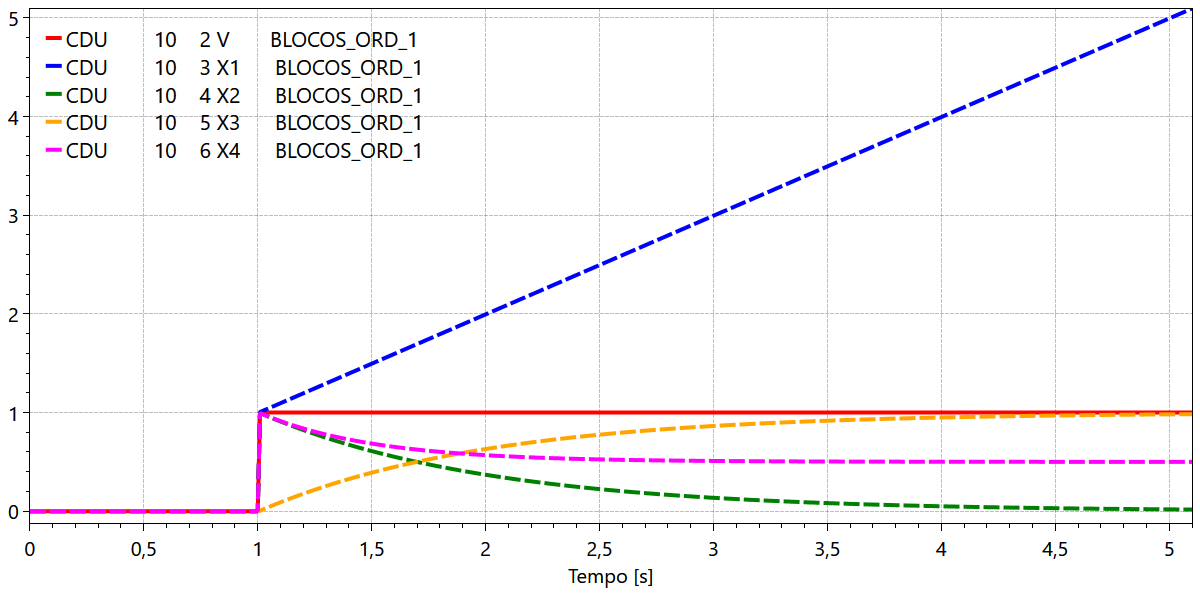
Fig. 96 Resposta ao degrau de blocos de primeira ordem¶
Nota
Observe que neste caso o valor de regime atingido por cada saída, após a aplicação de um pulso com amplitude V, pode ser avaliado por meio da aplicação do teorema de valor final da teoria de controle moderno 1.
Teorema do Valor Inicial: \(f(0^+) = \text{lim}_{t \rightarrow 0 } f(t) = \text{lim}_{t \rightarrow \infty } s F(s)\)
Teorema do Valor Final: \(f(\infty) = \text{lim}_{t \rightarrow \infty } f(t) = \text{lim}_{t \rightarrow 0 } s F(s)\)
- 1
Katsuhiko Ogata and Bernardo Severo. Engenharia de controle moderno. Prentice Hall do Brasil, 1998.