
Obtenção de Parâmetros da Curva de Saturação para Entrada de Dados no Anatem¶
O Anatem dispõe de quatro modelos de curvas predefinidos, por meio dos quais é possível modelar o efeito da saturação através de parâmetros a serem fornecidos pelo usuário, via código DCST e, posteriormente, relacionando-a à máquina em questão.
A curva de saturação de uma máquina síncrona pode ser representada por meio de funções por partes ou funções polinomiais. No caso do Anatem, para a curva modelo tipo 2, é utilizada a representação do Paul Anderson 1, função por partes, onde a função de saturação é dividida em duas funções, sendo a primeira linear e a segunda exponencial. Prabha Kundur 2 apresenta outra formulação por partes, onde existe uma terceira parte exponencial.
Nota
O modelo tipo 2 é o normalmente utilizado para a representação da saturação nas máquinas síncronas.
A curva do modelo tipo 2 do Anatem presume a entrada de três parâmetros (A, B, C). Os seguintes valores para esses parâmetros são tipicamente encontrados para o modelo tipo 2:
Obtenção dos parâmetros a partir das curvas de tensão terminal graficamente pela diferença visual na tensão¶
Uma curva de saturação típica pode ser encontrada na figura abaixo:
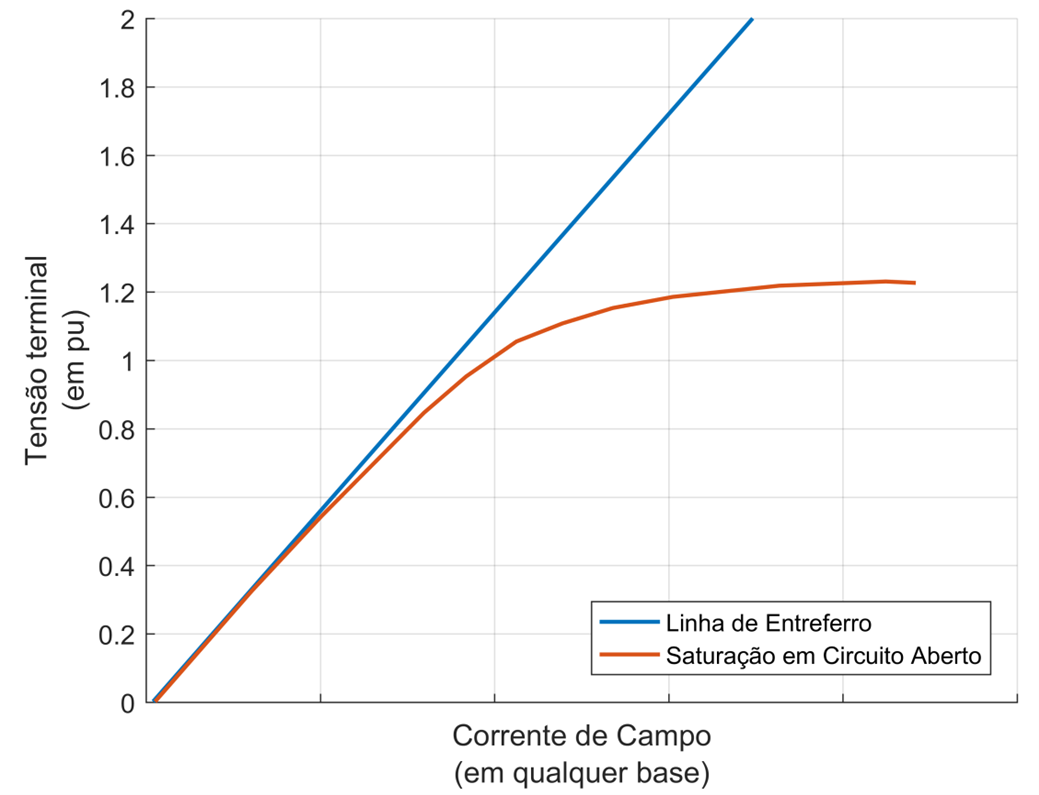
Fig. 111 Exemplo de curva de saturação informada pelo fabricante¶
A parte exponencial do modelo tipo 2 da curva de saturação do Anatem pode ser definida pelas seguintes expressões:
Sendo:
\(V_{gap}\) |
Tensão na linha de entreferro |
\(V_{sat}\) |
Tensão no circuito aberto com saturação |
O parâmetro C é utilizado para identificar o ponto de ruptura entre o modelo linear e o modelo exponencial. Normalmente, utiliza-se o valor de 0,8 para este parâmetro. Restam, portanto, dois parâmetros a serem definidos (A e B). Como a função exponencial é uma função monótona, dois pontos definem uma função exponencial que depende de dois parâmetros. Sendo assim, é preciso aquirir do gráfico da saturação da máquina dois pontos (sob a região exponencial).
Definimos as seguintes variáveis:
\(I_{f1}\) |
Corrente necessária para se obter 1,0 pu de tensão na linha do entreferro |
\(I_{f2}\) |
Corrente necessária para se obter 1,0 pu de tensão no circuito aberto com saturação |
\(I_{f3}\) |
Corrente necessária para se obter 1,2 pu de tensão no circuito aberto com saturação |
As correntes \(I_{f2}\) e \(I_{f3}\) podem estar definidas para quaisquer outros valores de tensão, mas usualmente esses são valores utilizados. A base dessas correntes é indiferente ao processo. Definindo essas correntes, calculamos S(1,0) e S(1,2) a partir dos valores das curvas no gráfico. A figura seguinte ilustra esse processo:
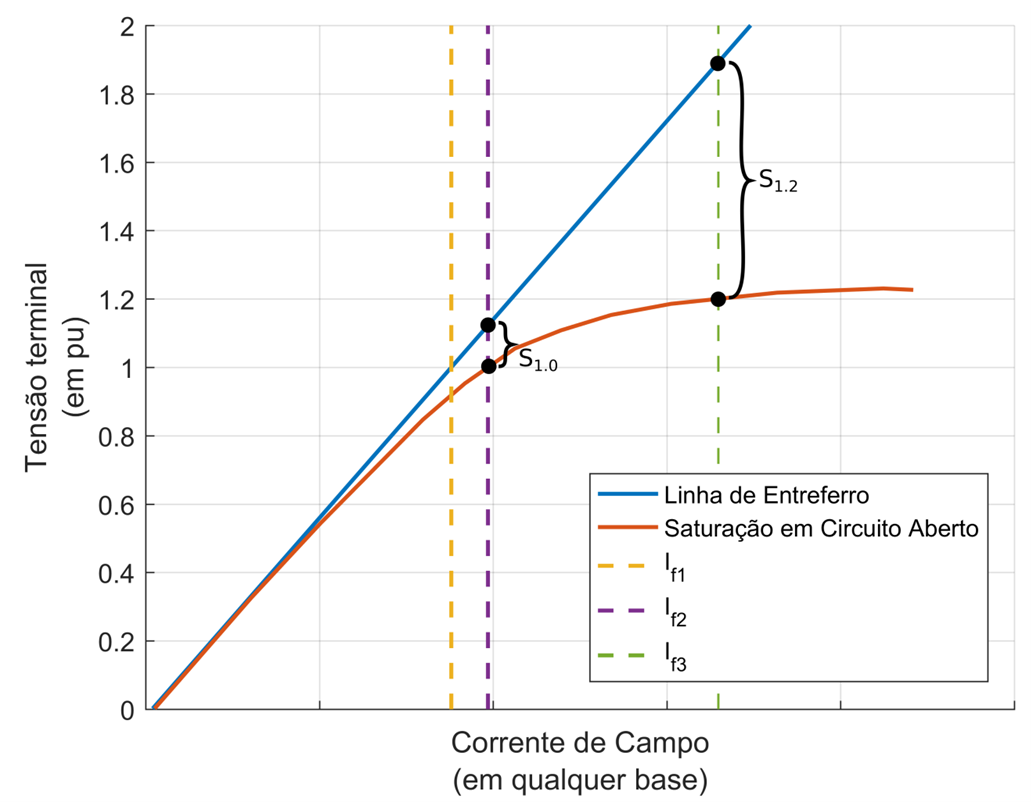
Fig. 112 Obtenção dos parâmetros para curva de saturação exponencial¶
Para as curvas utilizadas, as tensões na linha do entreferro para a corrente \(I_{f2}\) é de 1,125 pu, enquanto que para a corrente \(I_{f3}\) é de 1,89 pu. Tais informações foram obtidas diretamente do gráfico. Assim:
Sendo \(S_1\) e \(S_2\) dois pontos quaisquer da parte exponencial da curva, os parâmetros A e B podem ser encontrados a partir da relação desses dois pontos regidos pela equação (1):
Calcula-se, então:
No Anatem, esses parâmetros calculados seriam informados como no excerto abaixo:
1DCST
2(Nc) T ( P1 ) ( P2 ) ( P3 )
3( A B C
401 2 0.023 8.542 0.8
5999999
Obtenção dos parâmetros a partir das curvas de tensão terminal pelas correntes \(I_{fn}\)¶
Alternativamente, sabendo que a relação entre a tensão na linha do entreferro e a corrente de campo é linear, também seria possível estimar o valor da tensão no entreferro a partir do cálculo da inclinação da reta, pela corrente \(I_{f1}\). Supondo que as correntes \(I_{f1}=17,60\ A\), \(I_{f2}=19,70\ A\) e \(I_{f3}=32,92\ A\) são conhecidas e referentes às curvas da seção anterior, a equação (2) pode ser reescrita da seguinte maneira:
Sendo \(V_{sat}\left(I_{fd}\right)\) a tensão obtida, para uma dada corrente de campo, pela curva de saturação em circuito aberto. Como as correntes \(I_{f2}\) e \(I_{f3}\) se referem às tensões de 1,0 e 1,2 pu, respectivamente, têm-se que:
As equações (3) e (4) fornecem então os seguintes valores para os parâmetros A e B:
No Anatem, esses parâmetros calculados seriam informados como no excerto abaixo:
1DCST
2(Nc) T ( P1 ) ( P2 ) ( P3 )
3( A B C
402 2 0.021 8.60 0.8
5999999
Observe que as diferenças entre os parâmetros encontrados nos caso 1 e caso 2 são decorrentes da imprecisão inerente à aquisição por inspeção de dados de um gráfico. Funções logarítmicas e exponenciais também são fonte de imprecisões em função da alta sensibilidade numérica decorrente de arredondamentos praticados.
Obtenção dos parâmetros a partir de dados tabelados¶
Outra possibilidade para a obtenção dos parâmetros da curva de saturação no Anatem reside na situação em que os dados da curva de saturação são dados na forma de tabela, como a informada a seguir:
Tensão Terminal |
L.E. |
C.S. VAZIO |
|||
|---|---|---|---|---|---|
Vt (kV) |
Vt (pu) |
Ifd (pu) |
Ifd (A) |
Ifd (pu) |
Ifd (A) |
0 |
0 |
0 |
0 |
0 |
0 |
11.5 |
0.5 |
0.30572 |
350.0249 |
0.30787 |
352.4865 |
13.8 |
0.6 |
0.36686 |
420.0254 |
0.37147 |
425.3034 |
16.1 |
0.7 |
0.428 |
490.0258 |
0.4379 |
501.3605 |
18.4 |
0.8 |
0.48915 |
560.0376 |
0.5104 |
584.3672 |
20.7 |
0.9 |
0.55029 |
630.038 |
0.59592 |
682.2807 |
23 |
1 |
0.61143 |
700.0384 |
0.7094 |
812.2062 |
25.3 |
1.1 |
0.67258 |
770.0503 |
0.8829 |
1010.85 |
27.6 |
1.2 |
0.73372 |
840.0507 |
1.1853 |
1357.074 |
29.9 |
1.3 |
0.79486 |
910.0511 |
1.7643 |
2019.982 |
32.2 |
1.4 |
0.85601 |
980.063 |
2.9372 |
3362.859 |
34.5 |
1.5 |
0.91715 |
1050.063 |
5.3851 |
6165.509 |
Os dados apresentados podem estar tanto em pu (em relação a alguma base) quanto em suas grandezas originais. Para a tensão, é importante que seja utilizado o valor da tensão em pu na base de tensão da máquina. Para a corrente, é indiferente se será utilizado em pu ou em Ampères. Assim, o procedimento de cálculo é semelhante ao realizado na seção anterior:
Portanto:
Desta forma, no Anatem esses parâmetros calculados seriam informados como no excerto abaixo:
1DCST
2(Nc) T ( P1 ) ( P2 ) ( P3 )
3( A B C
43 2 0.035 7.66 0.8
5999999