Bloco POL(S)¶
O bloco POL(S) é utilizado em malhas de controle para representar funções de transferência com numerador e denominador formados por polinômios até a terceira ordem.
Características¶
# Entradas |
1 |
Sinal de Entrada |
Real |
Sinal de Saída |
Real |
Primeiro Registro
P1
Coeficiente do termo de terceira ordem do polinômio do numerador
P2
Coeficiente do termo de segunda ordem do polinômio do numerador
P3
Coeficiente do termo de primeira ordem do polinômio do numerador
P4
Coeficiente do termo independente do polinômio do numerador
Segundo Registro
P1
Coeficiente do termo de terceira ordem do polinômio do denominador
P2
Coeficiente do termo de segunda ordem do polinômio do denominador
P3
Coeficiente do termo de primeira ordem do polinômio do denominador
P4
Coeficiente do termo independente do polinômio do denominador
Valores default |
\(P_1^1=P_2^1=P_3^1=P_4^1=P_1^2=P_2^2=P_3^2=P_4^2=0\) |
Restrições |
Veja quadro a seguir* |
Aviso
* O denominador deve ter ordem \(\geq 2\) e obrigatoriamente maior ou igual que a ordem do numerador. Ao menos um dos termos independentes (\(P_4\)) deve ser não nulo.
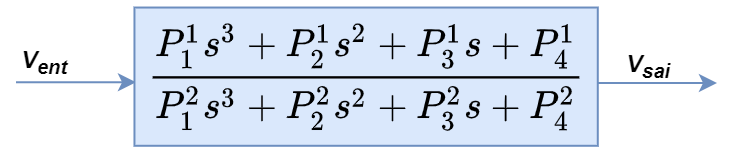
Lógica¶
\(A(t) = V_{ent}(t) - \frac{1}{D_k} \left( \sum_{i=0}^{k-1} D_i X_{i+1}(t) \right)\)
\(X_k (t) = X_k (0) + \int_{0}^{t} A(\xi) d\xi\)
\(X_i (t) = X_i (0) + \int_{0}^{t} X_{i+1}(\xi) d\xi\), com \(i = k-1,1\)
\(V_{sai} (t) = \frac{1}{D_k} \left( N_k A(t) + \sum_{i=0}^{k-1} N_i X_{i+1}(t) \right)\),
onde \(k\) é a ordem do denominador e \(x_i\), com \(i=1\), e \(k\) são as variáveis de estado.