
Métodos de Solução usados no Programa¶
O método matemático de solução utilizado no Anatem é dividido em dois conjuntos de problemas principais: a solução das equações diferencias e a solução das equações algébricas.
São utilizadas equações diferenciais para descrever o comportamento da maioria dos equipamentos (como as máquinas síncronas e seus controles), enquanto que as equações algébricas são utilizadas para descrever o comportamento da rede elétrica e de parte da modelagem dos equipamentos (como blocos de CDU algébricos).
Método de Integração para Equações Diferenciais¶
O programa utiliza o método trapezoidal implícito para a algebrização das equações diferenciais, cuja formulação básica está definida a seguir para uma equação diferencial de primeira ordem:
Assim:
Sendo \(B_{(t-\Delta t)}\) chamado de “termo histórico” e definido como:
Método de Solução das Equações Algébricas da Rede CA¶
É utilizado o método direto de solução de sistemas lineares usando fatoração LU em sistemas esparsos de matrizes simétricas. A rede CA é descrita pelo sistema linear do tipo \([Y_\text{bus}] [V] = [I]\), onde \([V]\) é o vetor de tensões nodais, \([I]\) é o vetor de correntes injetadas nos nós e \([Y_\text{bus}]\) a matriz de admitância nodal. Caso haja cargas funcionais ou outros elementos não lineares (como conversores CA-CC, compensadores estáticos, motores de indução, etc.) as correntes destes elementos são consideradas no vetor \([I]\) e a solução de rede será necessariamente iterativa, pois estas correntes dependem do vetor de tensões \([V]\) a ser calculado. As barras de geração consideradas como barras infinitas (tensão e frequência constantes) têm as variáveis correspondentes eliminadas do sistema, sendo suas contribuições incluídas no termo independente à direita da igualdade do sistema.
Nota
Barras swing (ou \(V\Theta\)) na modelagem do fluxo de potência não possuem relação com barras infinitas em transitórios eletromecânicos.
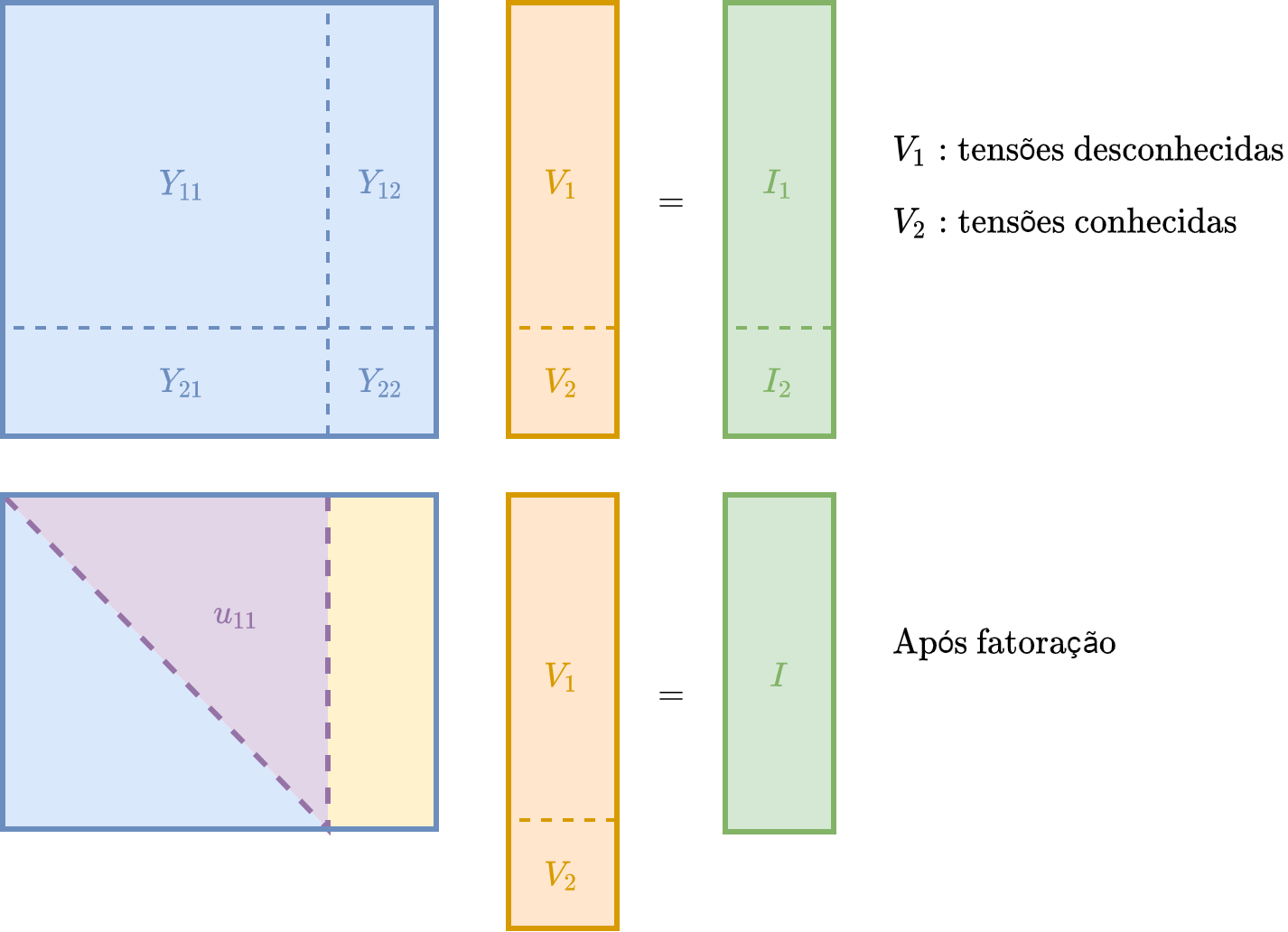
Fig. 103 Esquema de fatoração utilizado na solução da Rede CA¶
Esquema de Solução do Anatem¶
Para a modalidade de simulação de transitórios eletromecânicos (código EXSI), o Anatem segue o fluxograma da Fig. 104. Existem quatro tipos de críticas realizadas pelo programa antes do processo de solução:
Consistência dos dados: entrada de dados inválida ou ausência de dados obrigatórios (como parâmetros obrigatórios de alguns blocos de CDU)
Associação inválida: quando o dado informado é referente a um elemento inexistente no fluxo de potência (para definir um motor de indução no Anatem, é necessário antes definir o motor no Anarede.
Interface de CDU inválida: quando os locais de medição informados não existem no caso, sejam eles relativos a dados do fluxo de potência (como circuitos), sejam eles relativos a equipamentos com dinâmica (como máquinas síncronas).
Inicialização inviável: quando as condições operativas observadas no caso do fluxo de potência são incompatíveis com os dados informados nos modelos dinâmicos (e.g., quando o reativo gerado por um gerador é superior no caso Anarede àquele verificado como possível pelo seu regulador de tensão).
Após a análise crítica dos dados, o Anatem prossegue com a simulação. A cada avanço no passo de simulação:
Avaliação de alterações no sistema: verifica-se condições de mudança no sistema (e.g., abertura de circuitos) devido a eventos ou à atuação de proteções;
Cálculo de termos históricos e Extrapolação quadrática: calcula-se o termo \(B_{(t-\Delta t)}\) e se realiza a extrapolação quadrática de variáveis de interesse. A extrapolação quadrática do Anatem aprimora a taxa de convergência do processo iterativo.
Solução iterativa das equações algébrico-diferenciais: todos os modelos de equipamentos e de rede são resolvidos nesta etapa. Este processo é iterativo e alternado. O detalhamento desta etapa se encontra na Fig. 105.
Relatórios e Plotagens: são emitidos nos arquivos OUT, LOG e PLT os dados referentes aquele passo de simulação (como atuação de eventos, controles, problemas de convergência, etc.).
A simulação finda quando é alcançado o tempo determinado no código DSIM imediatamente anterior à execução do código EXSI.
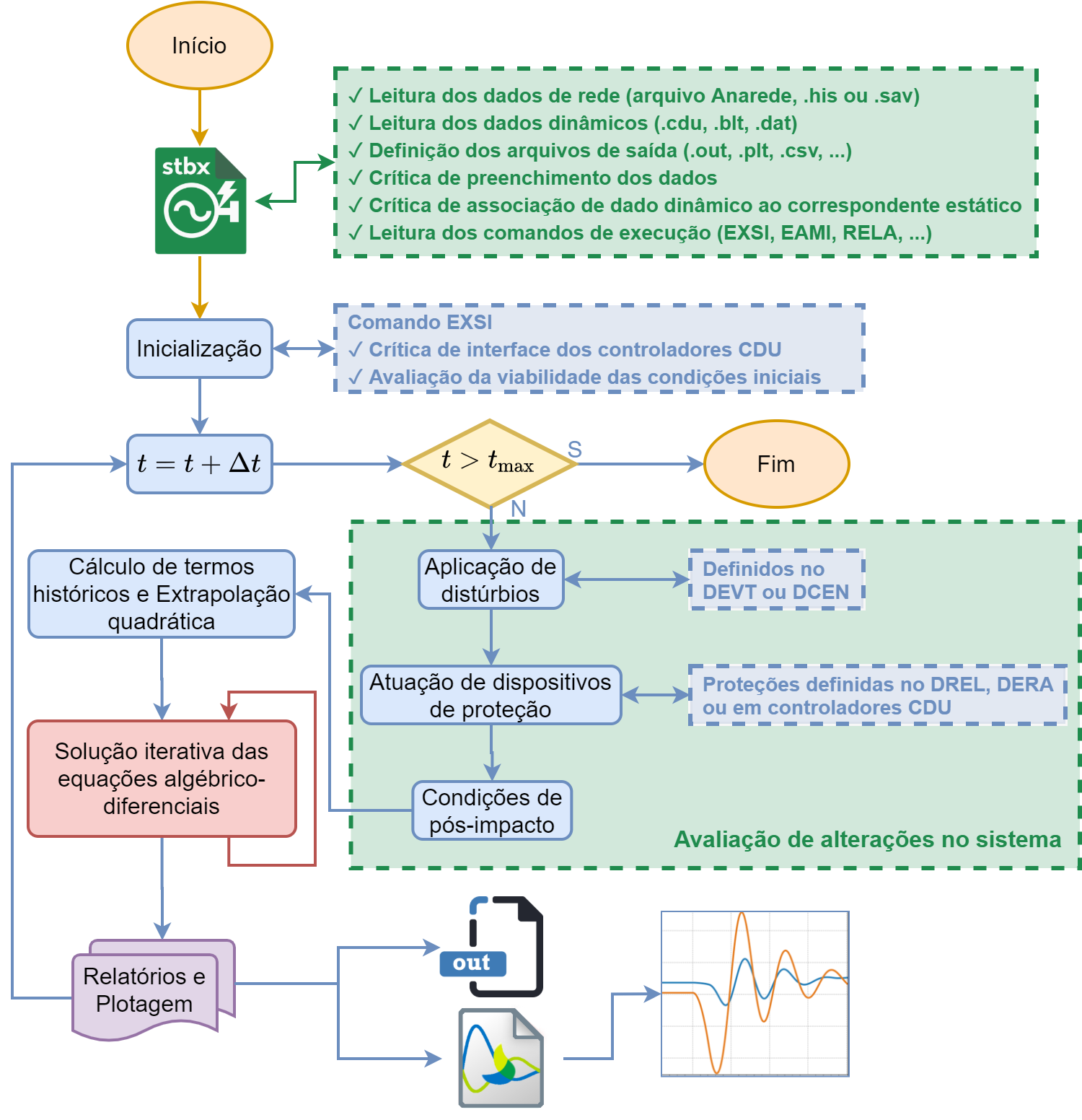
Fig. 104 Fluxograma da solução do problema de estabilidade eletromecânica no Anatem¶
O detalhamento da solução do processo iterativo pode ser divido em quatro partes:
Solução de modelos CC: corresponde a solução matemática de modelos de controle de elo e também de conversores CA-CC. As equações diferenciais desses modelos são resolvidas pelo método trapezoidal implícito, de forma alternada com as equações algébricas associadas.
Solução de rede CC: corresponde a solução matemática da rede CC. A rede CC é considerada modelada por elementos estáticos e portanto não apresenta modelagem diferencial nas suas equações. Estas equações algébricas são resolvidas de forma simultânea pelo método LU.
Solução de modelos CA: corresponde a solução matemática de praticamente todos os modelos dinâmicos como geradores síncronos e compensadores estáticos. As equações diferenciais desses modelos são resolvidas pelo método trapezoidal implícito, de forma alternada com as equações algébricas associadas.
Solução de rede CA: corresponde a solução matemática da rede CA. A rede CA é considerada modelada por elementos estáticos e portanto não apresenta modelagem diferencial nas suas equações. Estas equações algébricas são resolvidas de forma simultânea pelo método LU.
Cada uma das etapas descritas anteriormente apresentam laços distintos de convergência, com constantes que alteram o processo de solução.
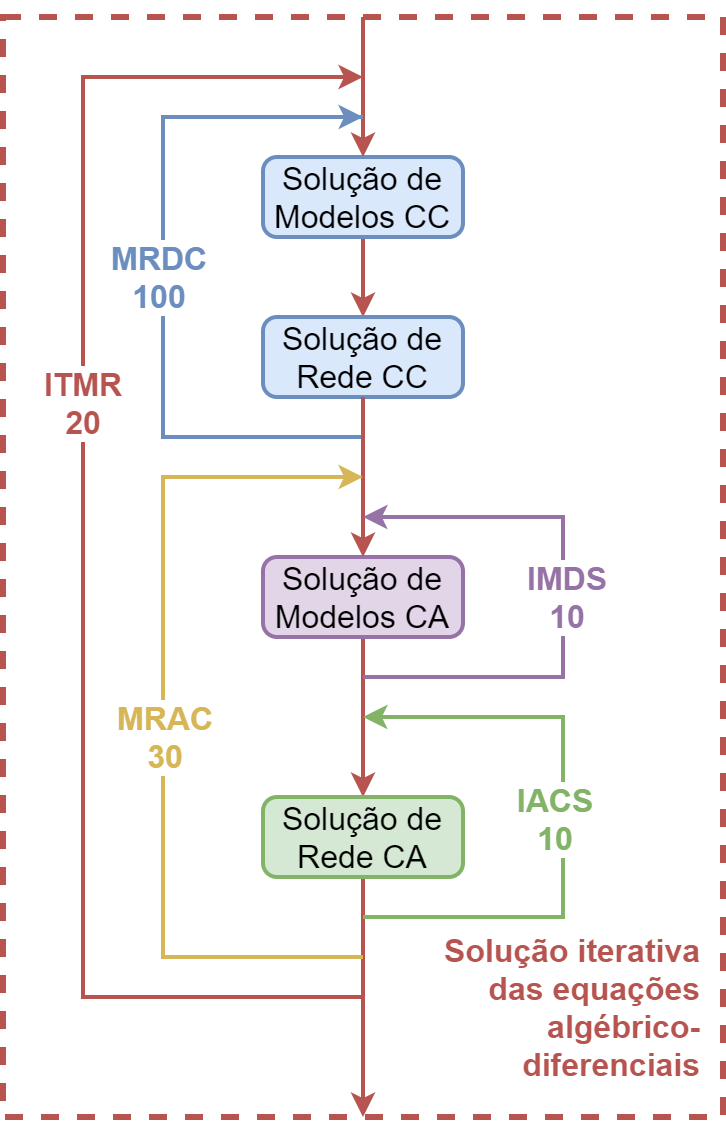
Fig. 105 Detalhamento da solução iterativa das equações algébrico-diferenciais¶
Ver também
Consulte a entrada Solução de Problemas de Convergência e de Desempenho para mais informações sobre o uso de Opções de Execução para alterar o comportamento do processo de solução do programa.